.:: Spring Mass Model of Electricity ::.
A purely mechanical model of electricity
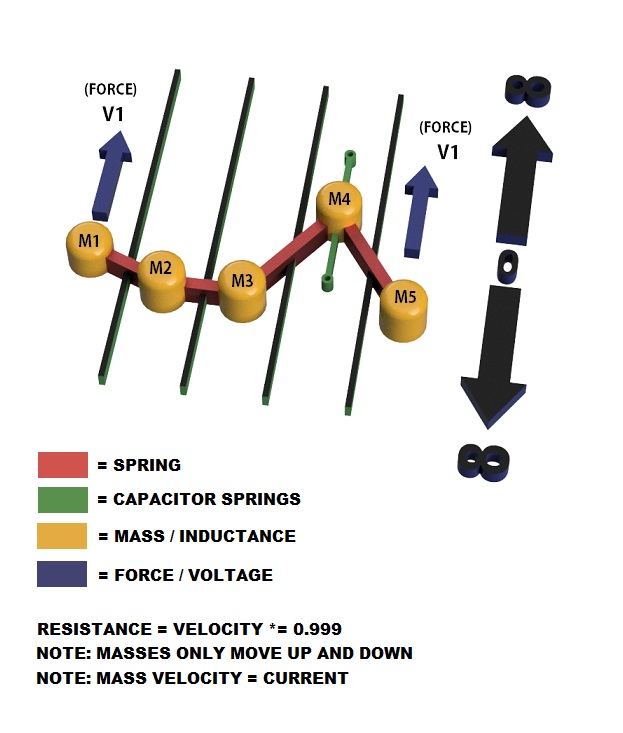
I wanted to write a program in C# for simulating electrical circuits. I initially didn't know where to begin. I needed to make a scalable model which was both simple, yet all inclusive. After a whole day of thinking, I finally came up with a mechanical model that can perfectly mirror all electrical properties and was easy to simulate (Hooke's Law and 1 dimension particle simulation)... resistance, capacitance, inductance, diode component, and signal propagation.
Above is the diagram of the mechanical model.
Each mass has inertia just like an inductor. When you apply a voltage (force) to an inductor (mass) it takes time for the current (mass velocity) to build up through it. When you remove the voltage (force), the current (mass velocity) tries to continue flowing. The speed of each mass represents current in the finite element of wire. Each mass is connected to its neighbor by a spring. When a mass begins to move up, it starts to pull its neighbor up as well (with subtle latency). To simulate a capacitor, you need to anchor one of the masses with a spring. When you start pulling the anchored mass it begins to move but then slows down and stops. This is just like charging a capacitor using a DC power source. Current begins to flow freely but as the capacitor becomes charged the current comes to a stop eventually. Inductance (mass inertia) blocks AC. Capacitance (anchored mass) blocks DC, just like actual electronics. Resistance is the same as multiplying a mass velocity by a coefficient that has a value of less than one. You can also simulate a diode by only letting the masses move in one direction. Because of the latency between each mass interaction by means of spring, you can see signals propagate, just like in real life. To form a closed circuit, you must connect the left most mass to the right most mass.
Resistance: Mass velocity = mass velocity X Resistance Coefficient
Capacitance: Spring anchored mass
Inductance: Mass inertia
Diode: Let mass only move in one direction
Switch: Resistor of high value, when button contacts are open
Some issues with the model... If current is constant the mass location will go off into infinity and the computer program will crash due to the overflow. A solution for this is to make the motion circular instead of linear, how ever this adds more complexity.
I am also unable to figure out how to model parallel circuits. If you figure it out please let me know.
SAMPLE SIMULATION CODE, NOT SURE IF IT WORKS THOUGH. RESISTANCE EFFECT VARIES WITH DELTA TIME.
CAPACITANCE VALUE IS LOWERED BY INCREASING THE COEFFICIENT.
LATEST CODE, YOU CAN SIMULATE A CLOSED LOOP OR A TRANSMISSION LINE.
GUI VERSION SIMULATOR
DOWNLOAD C# GUI VERSION (CODE AND EXE)
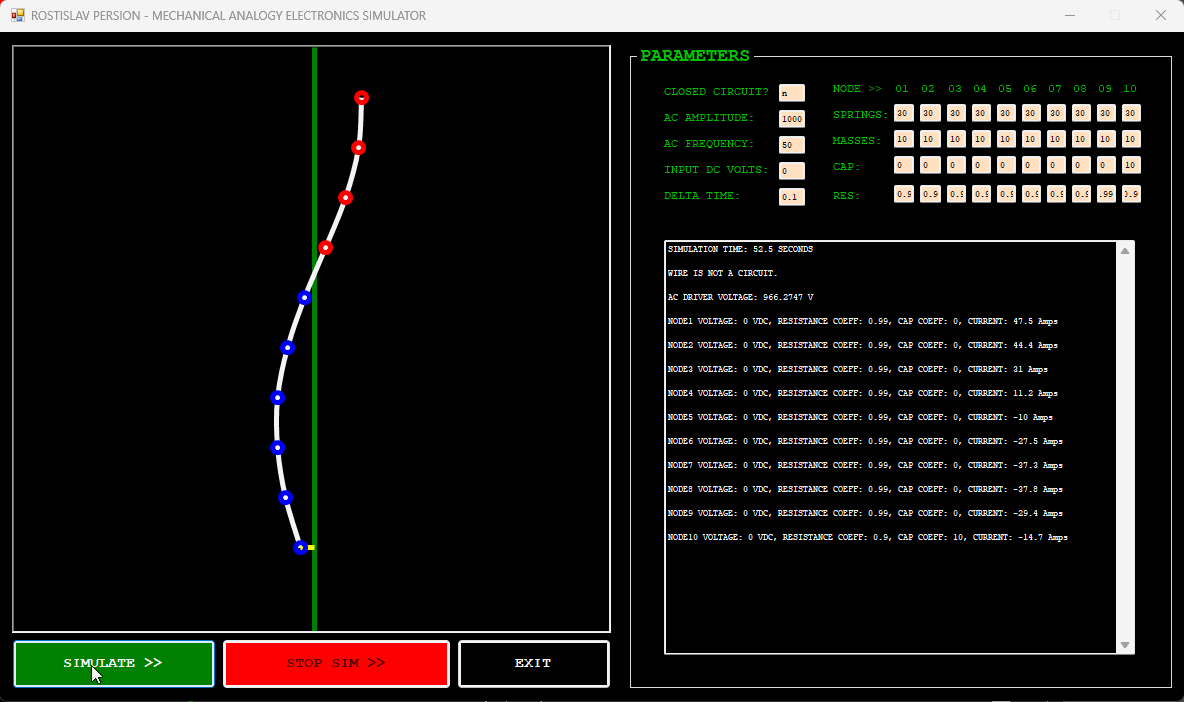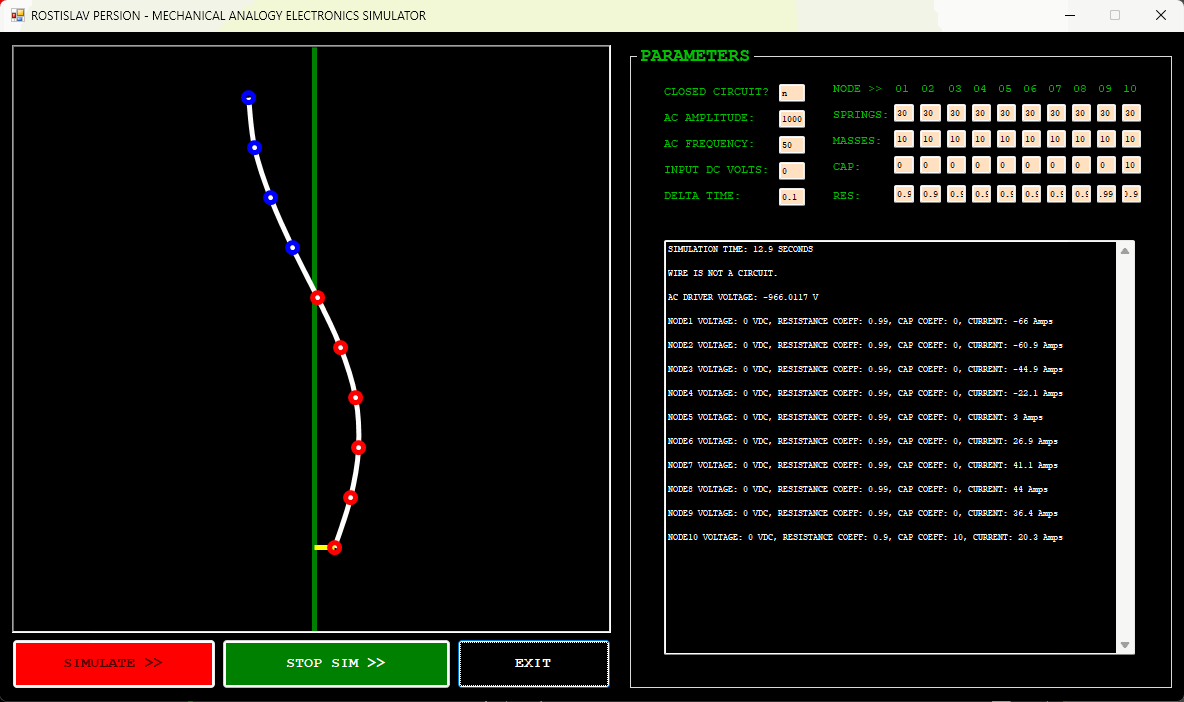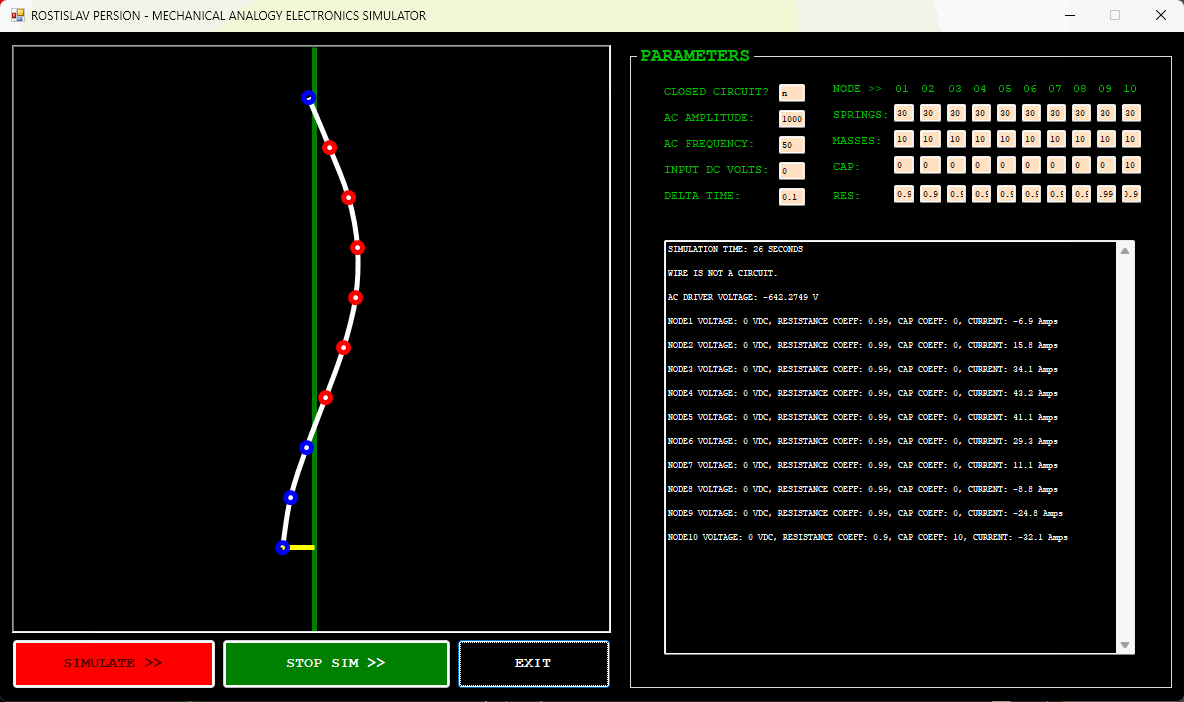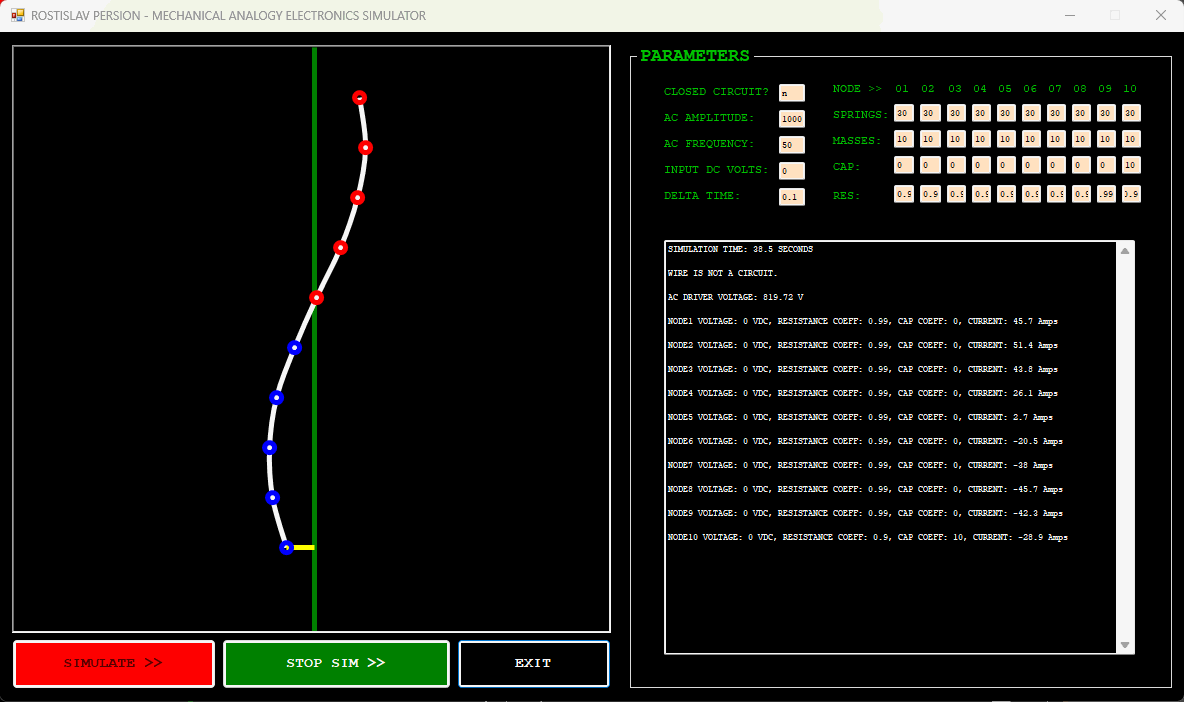
IMPEDANCE MISMATCH EXAMPLE (NODE 1 IS AC DRIVER, NODE 10 IS DUMMY LOAD, OPEN CIRCUIT)
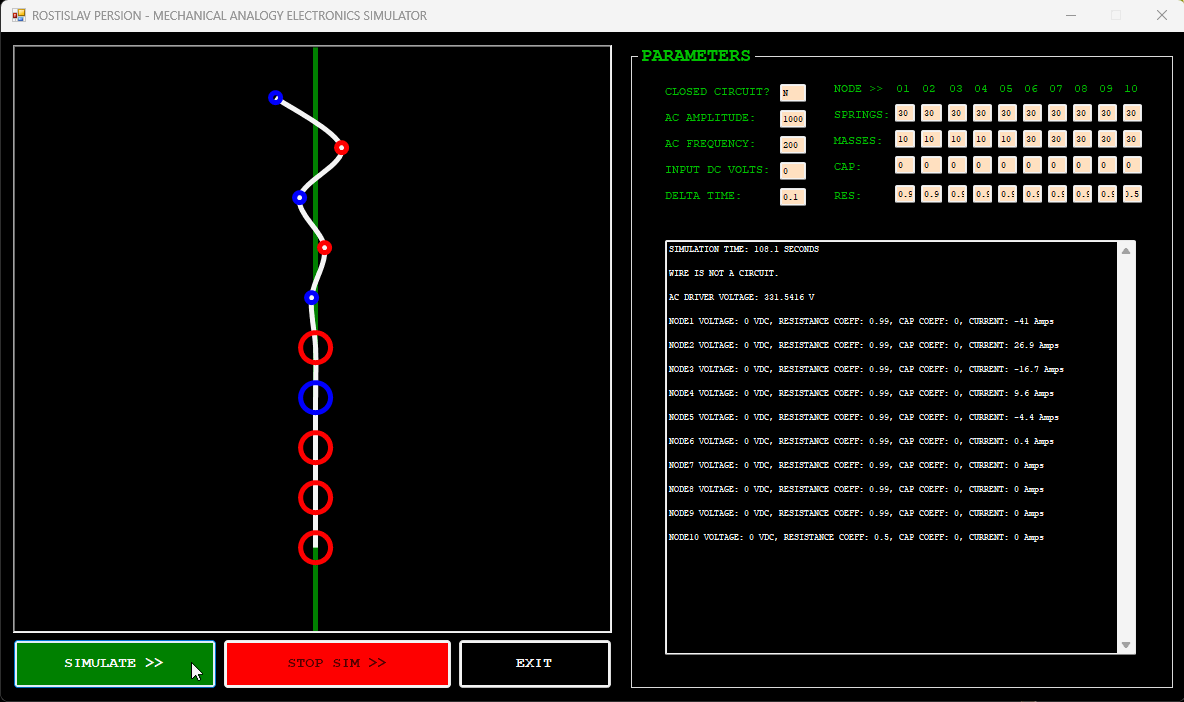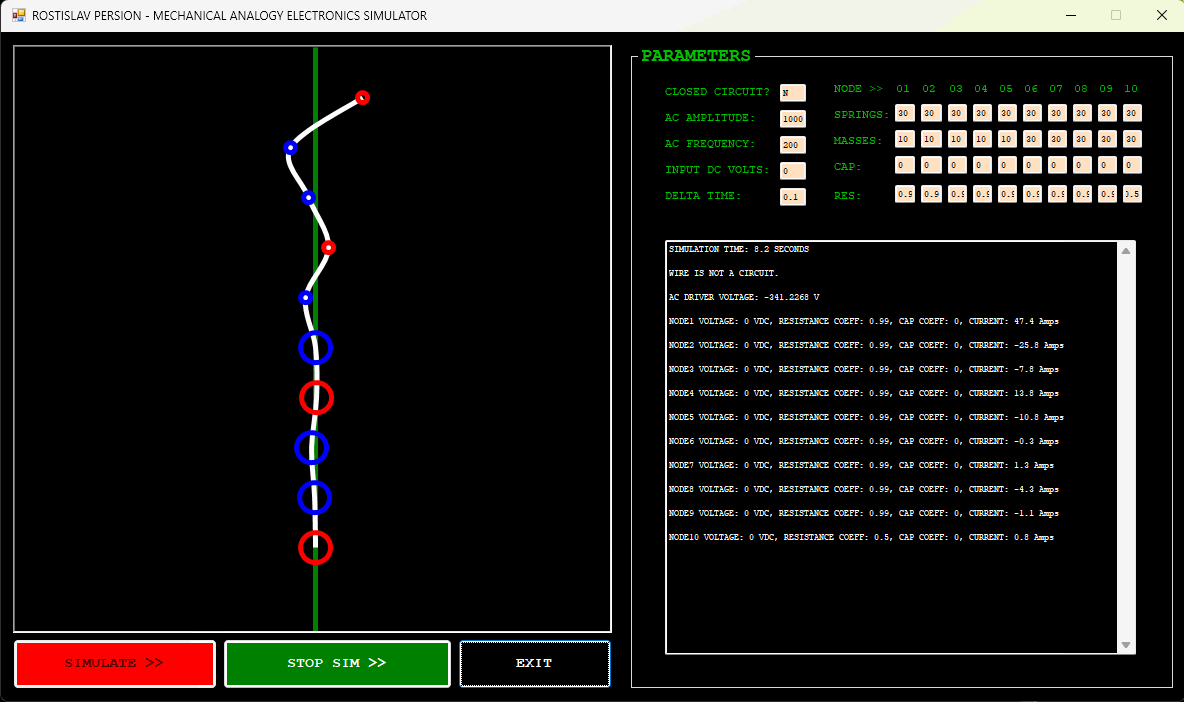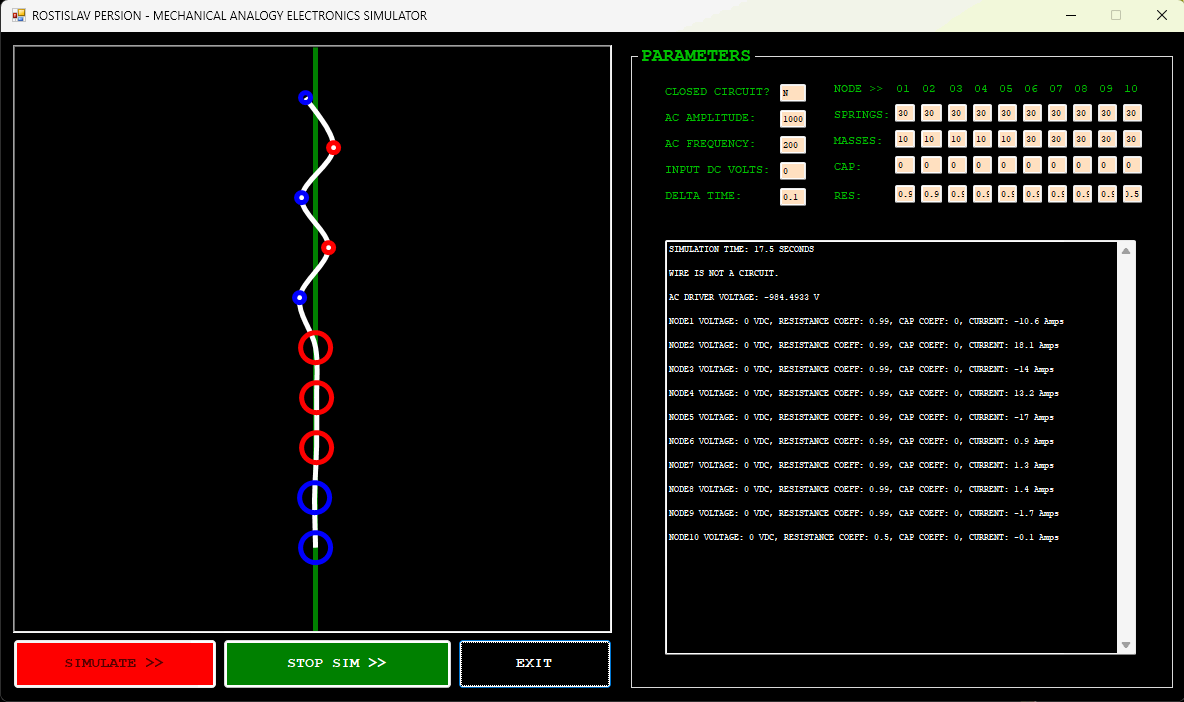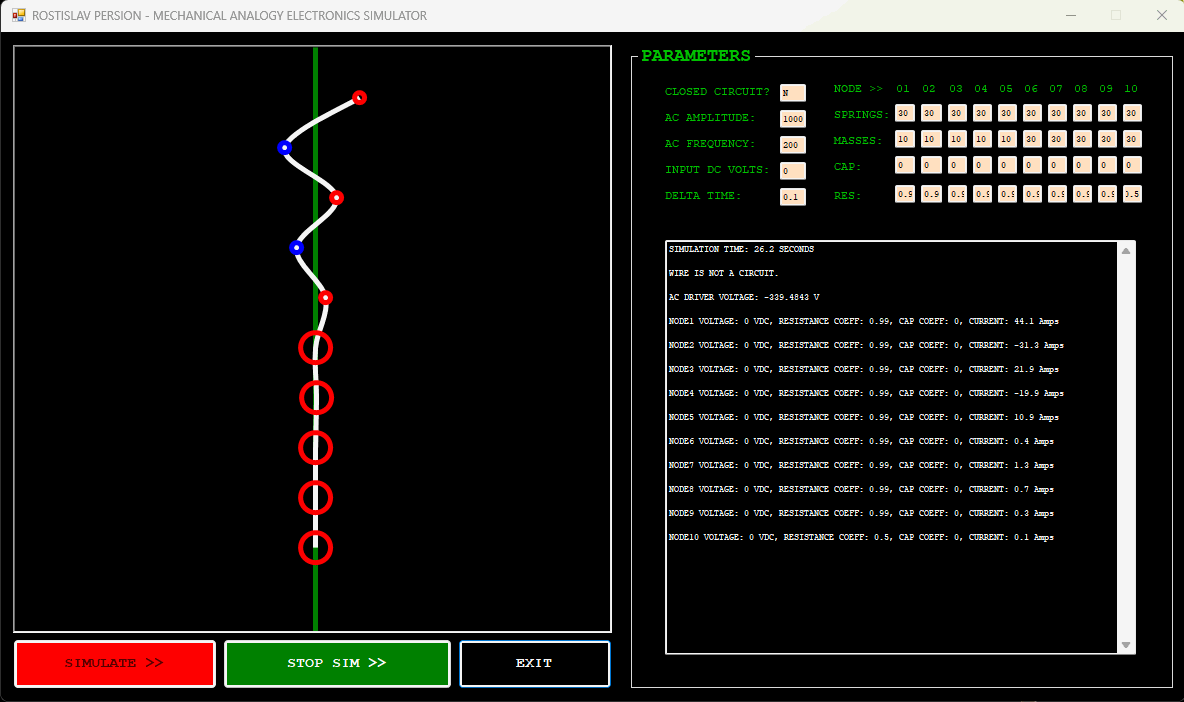
IMPEDANCE TRANSFORMER EXAMPLE (NODE 1 IS AC DRIVER, NODE 10 IS DUMMY LOAD, OPEN CIRCUIT)
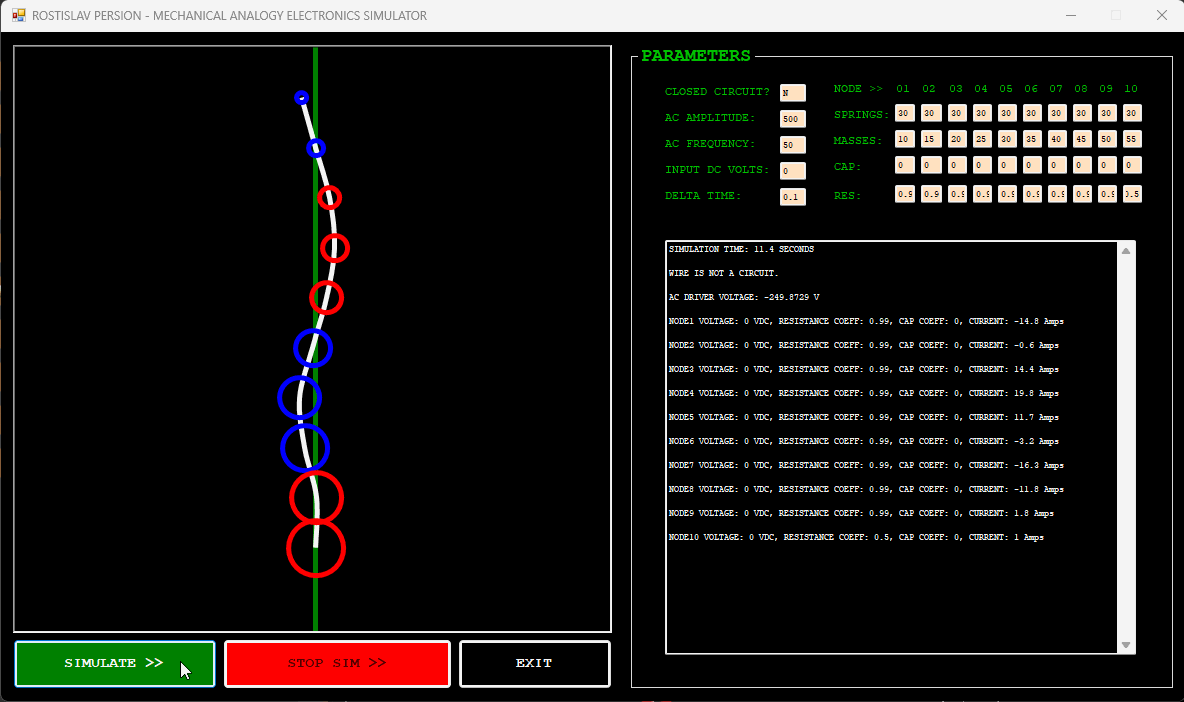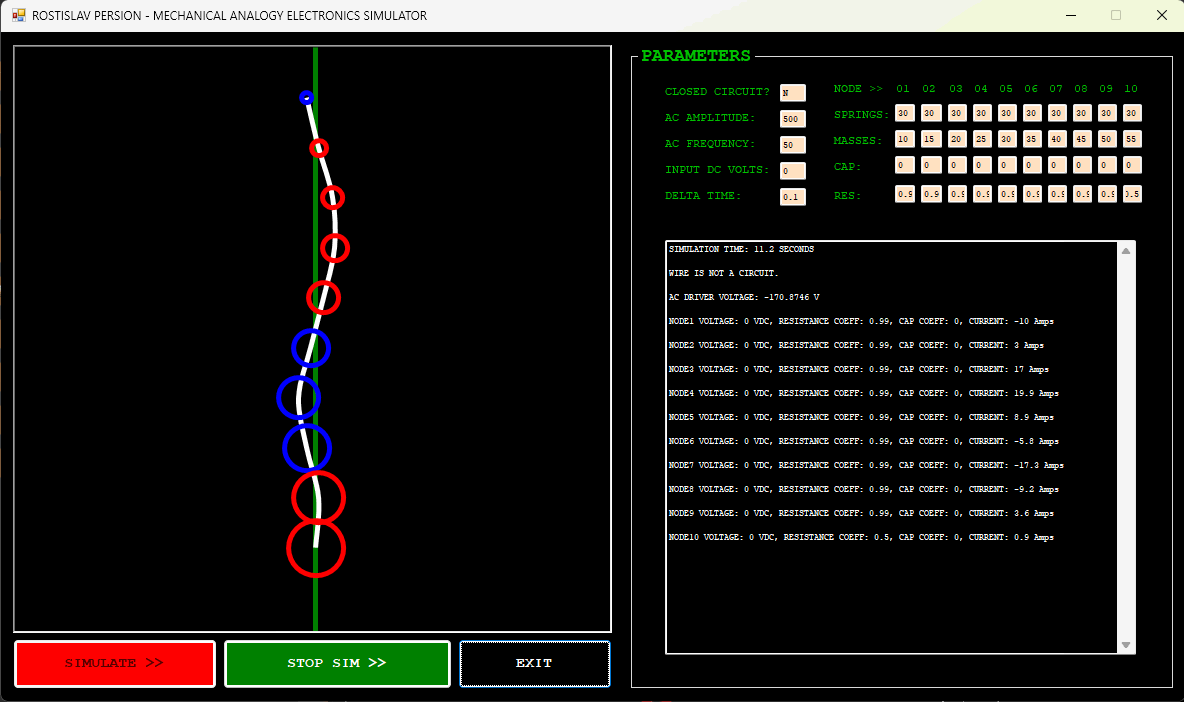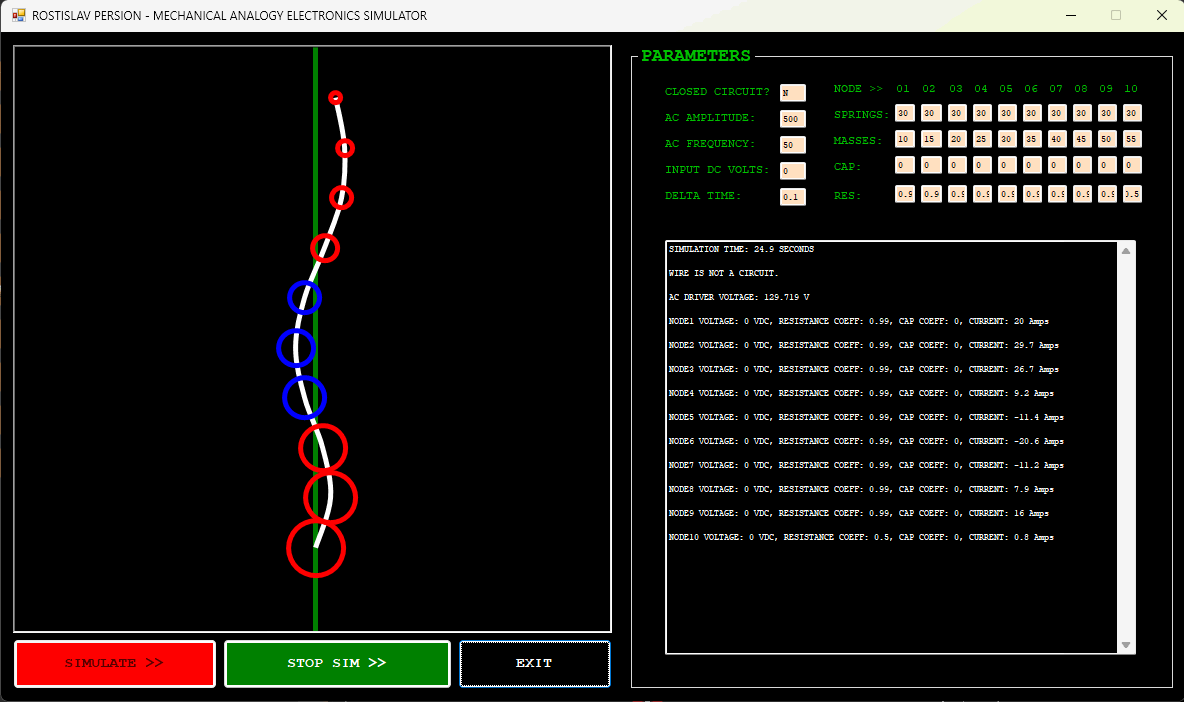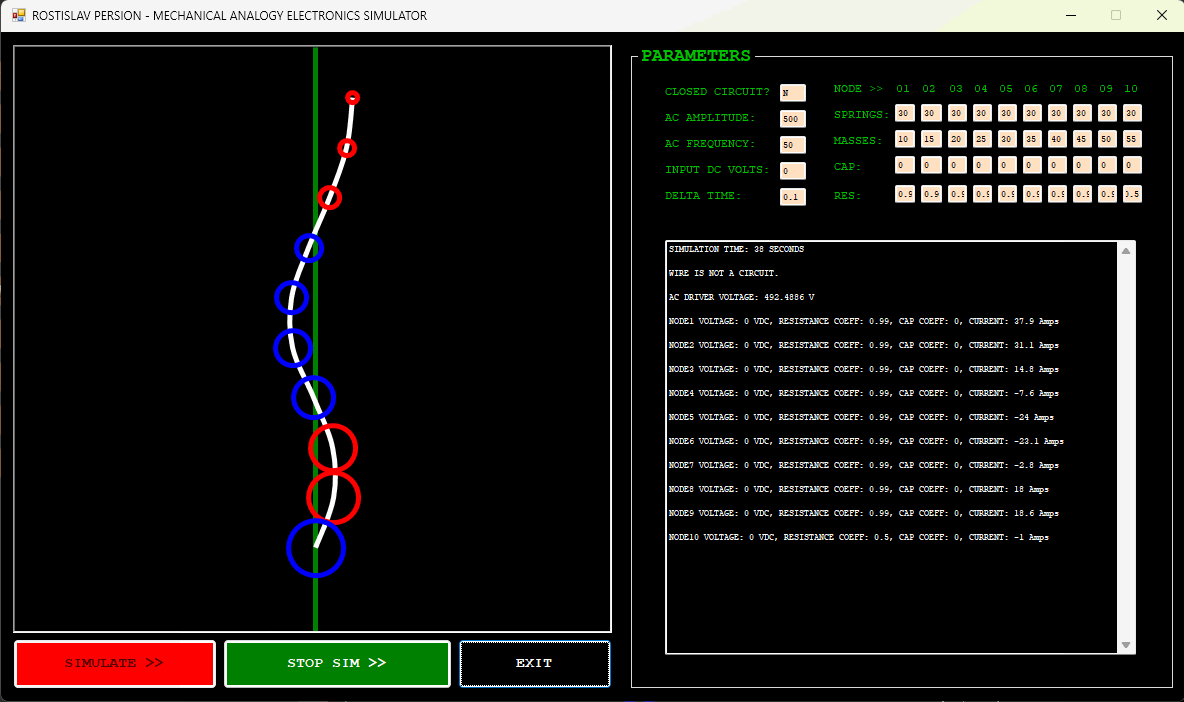
DC CURRENT EXAMPLE (NODE 1 IS DC DRIVER, CLOSED CIRCUIT)
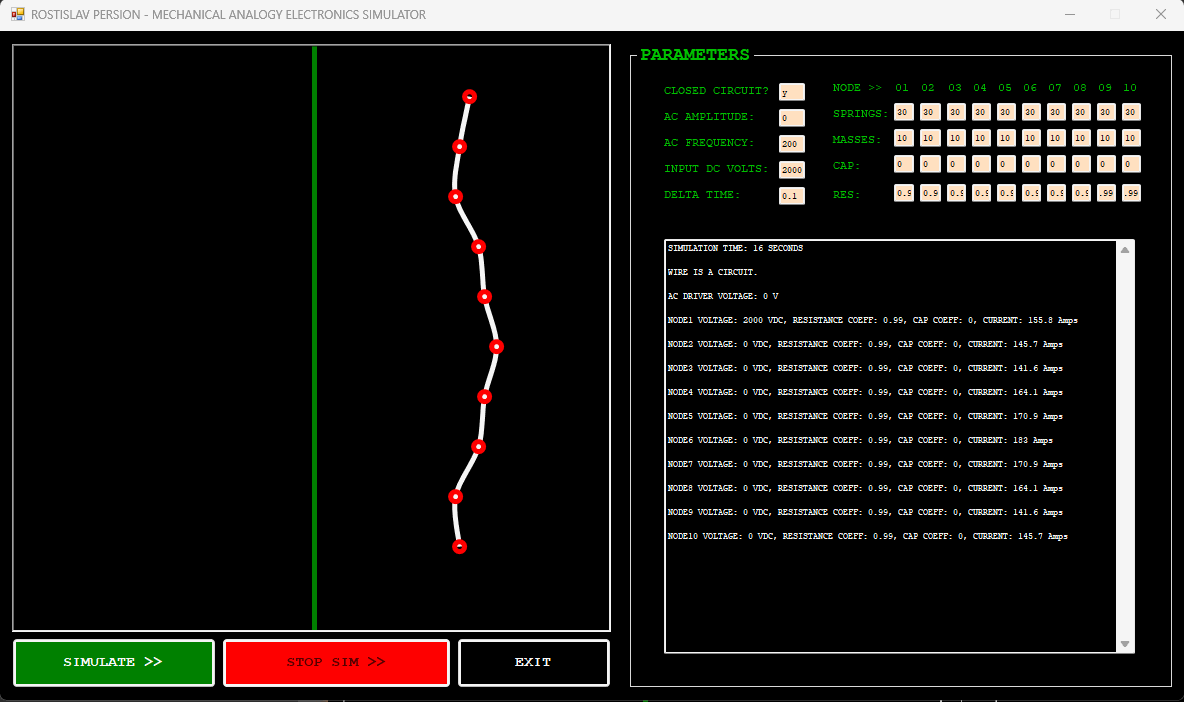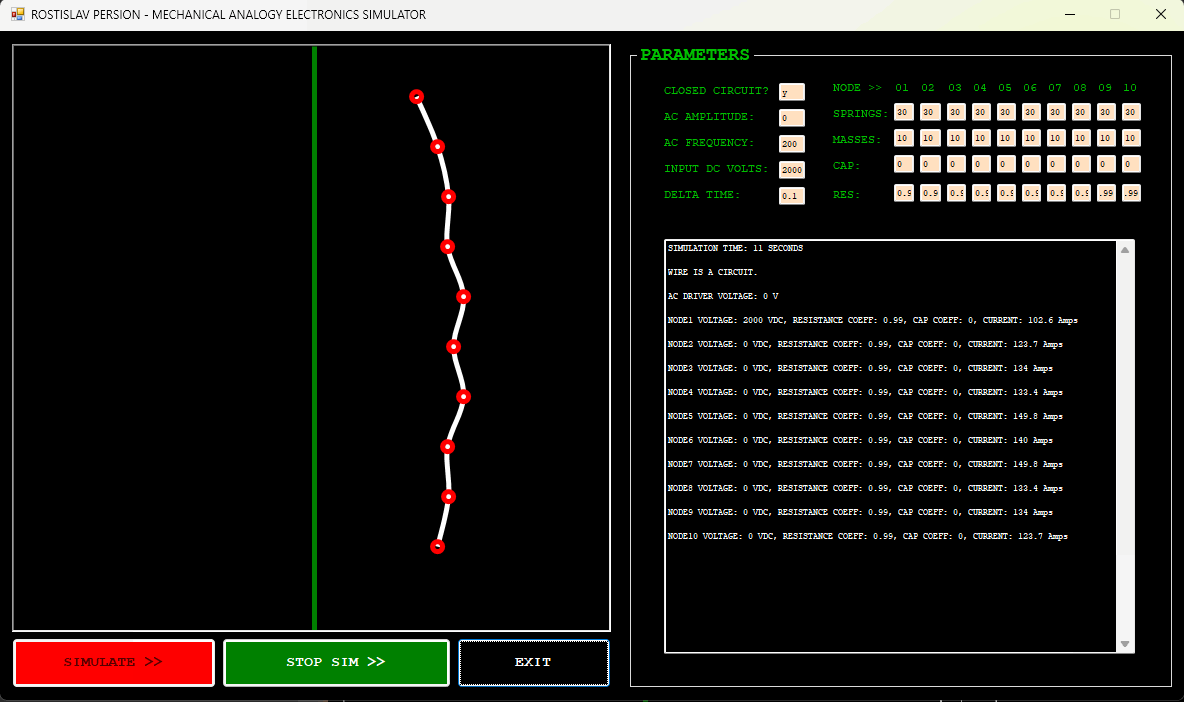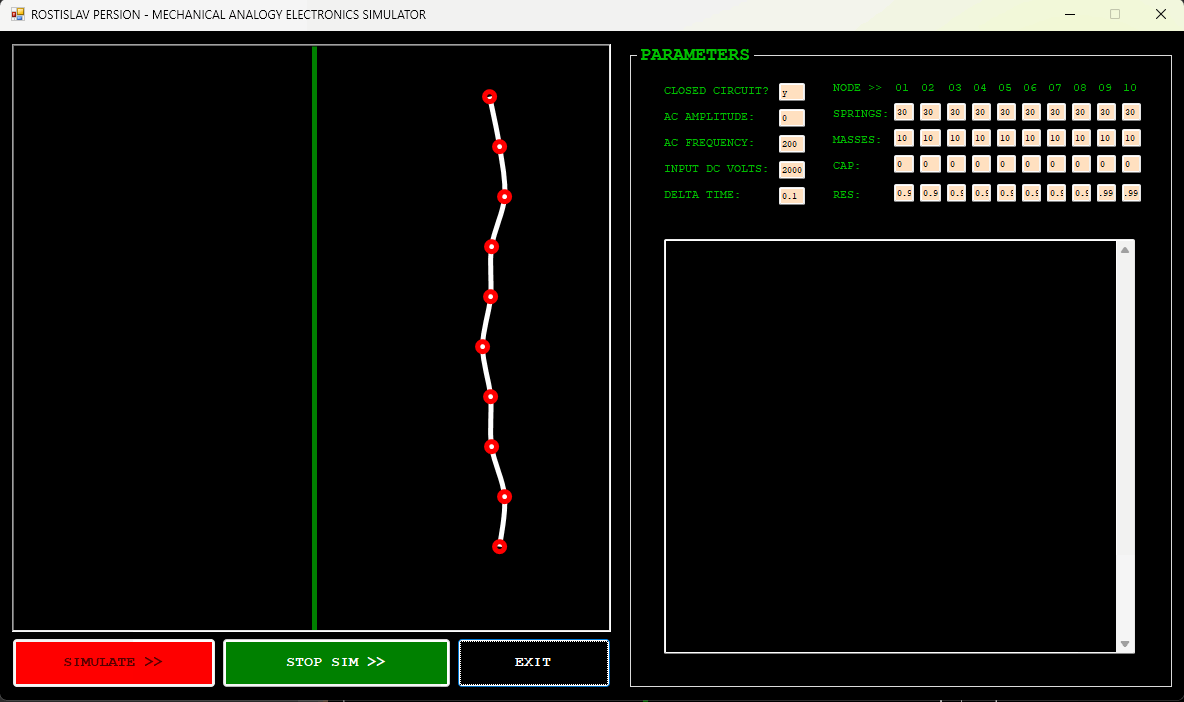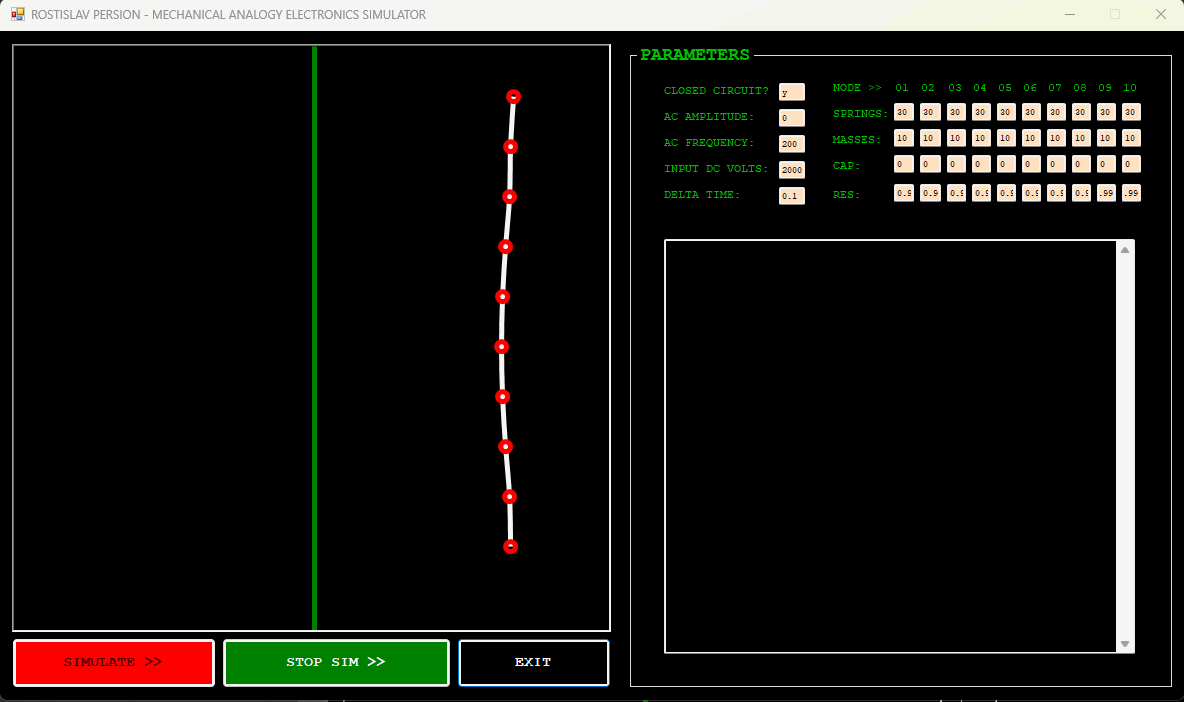
AC CURRENT EXAMPLE (NODE 1 IS AC DRIVER, CLOSED CIRCUIT)
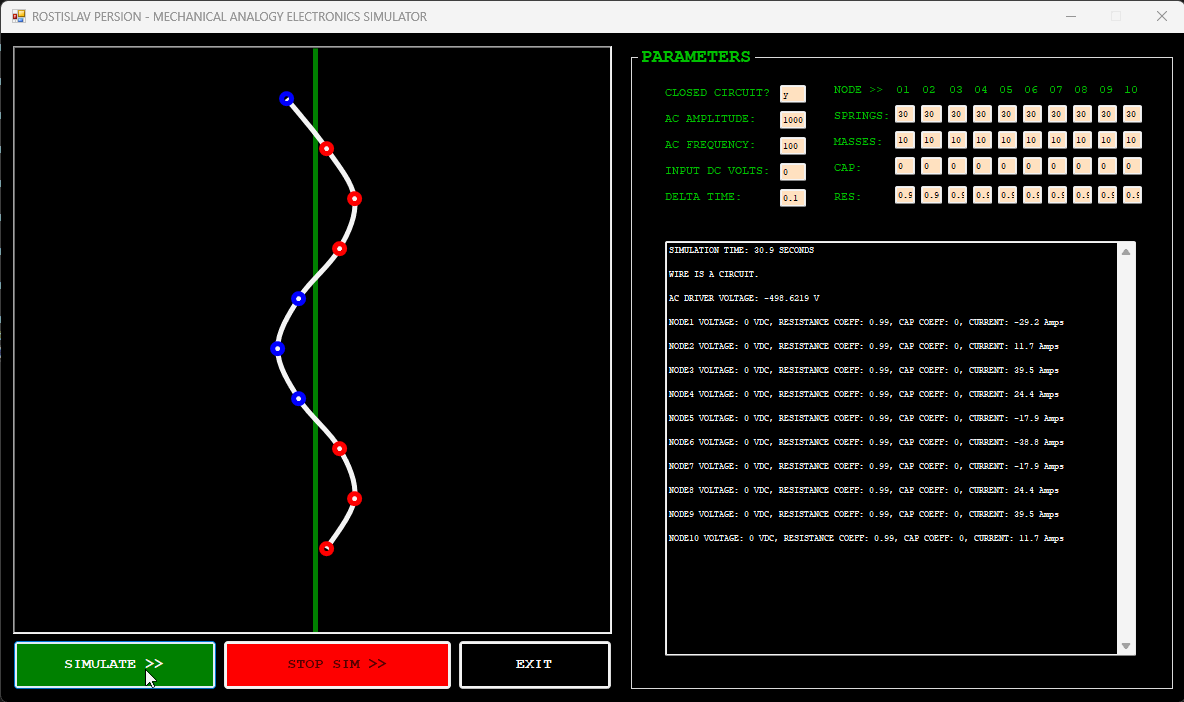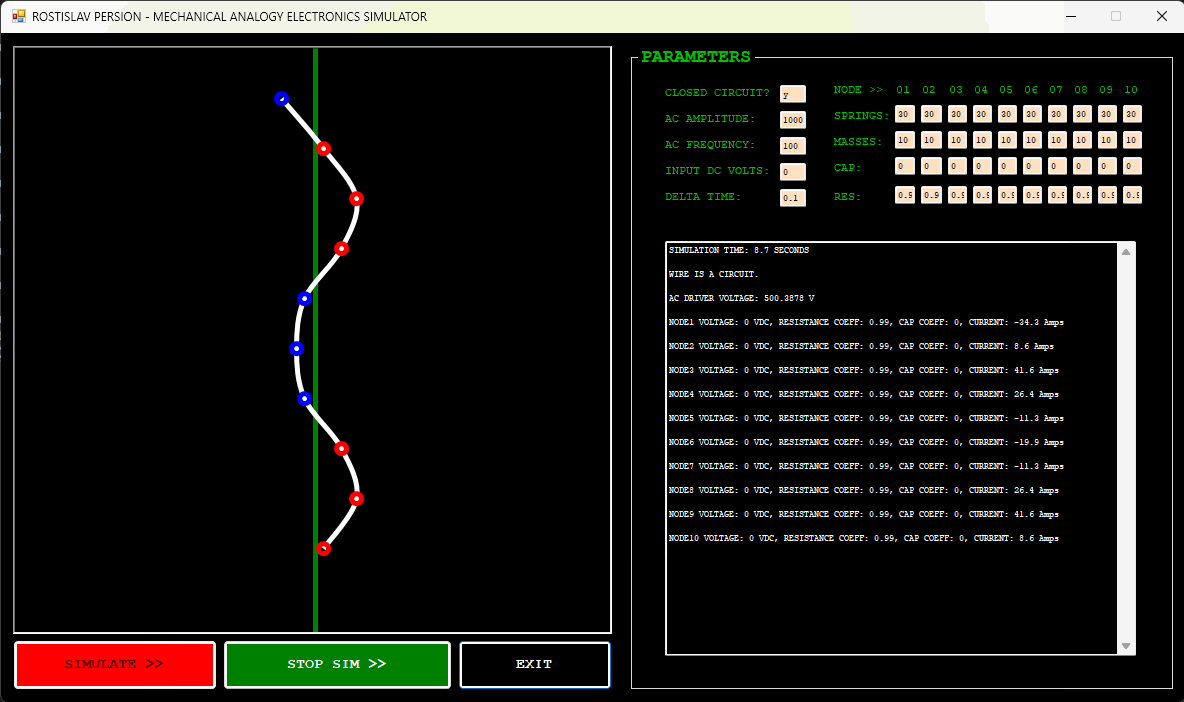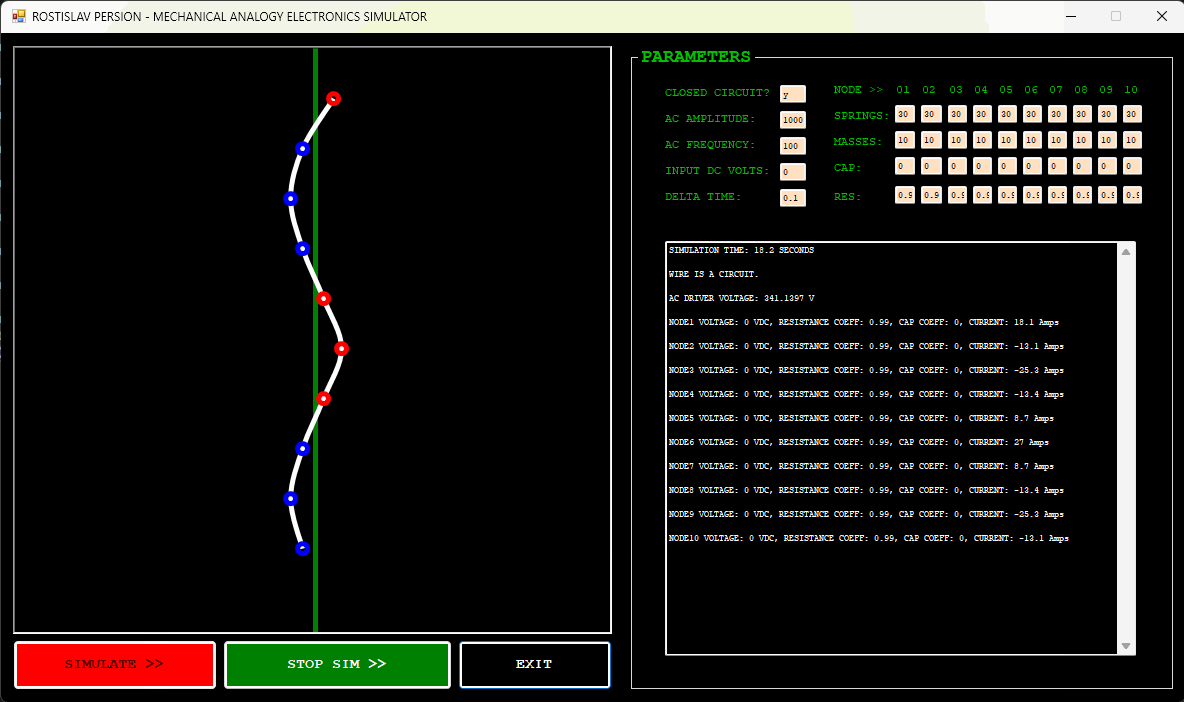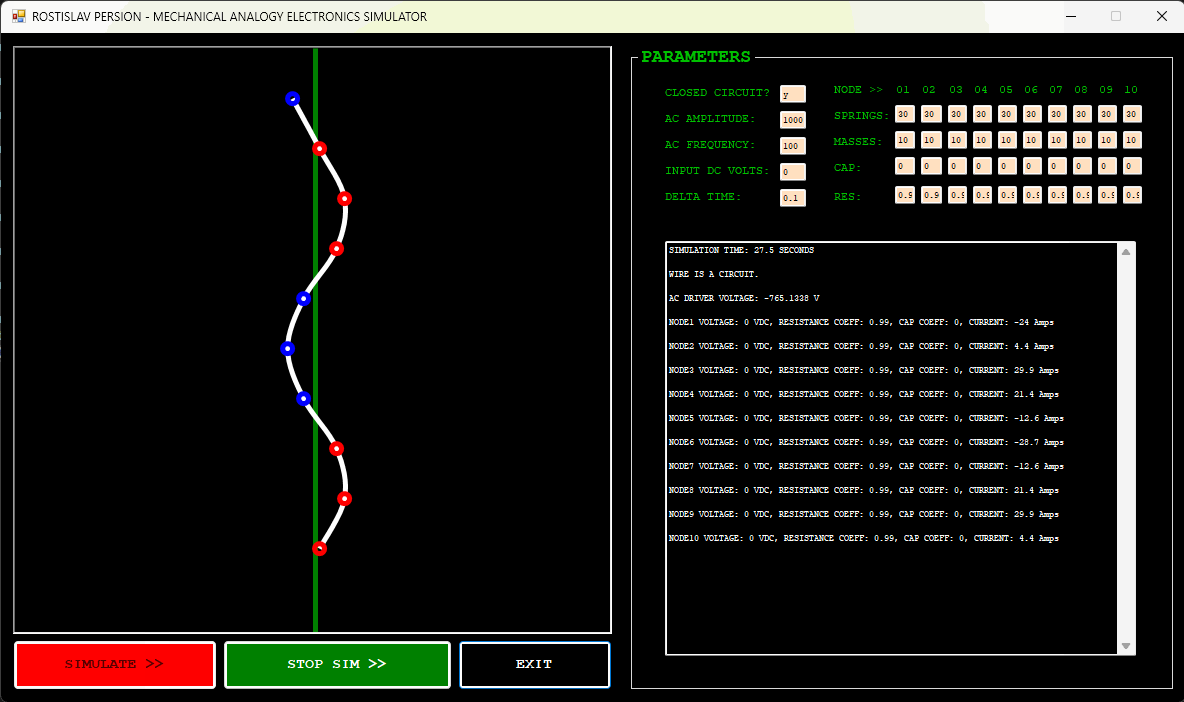
DUMMY LOAD EXAMPLE EXAMPLE (NODE 1 IS AC DRIVER, NODE 10 IS DUMMY LOAD, OPEN CIRCUIT)
CONSOLE VERSION SIMULATOR
CLOSED CIRCUIT DC (# = NODE CURRENT)
SOME SIMULATION VARIABLES WERE CHANGED IN THE CODE, NOT THE USER INPUT
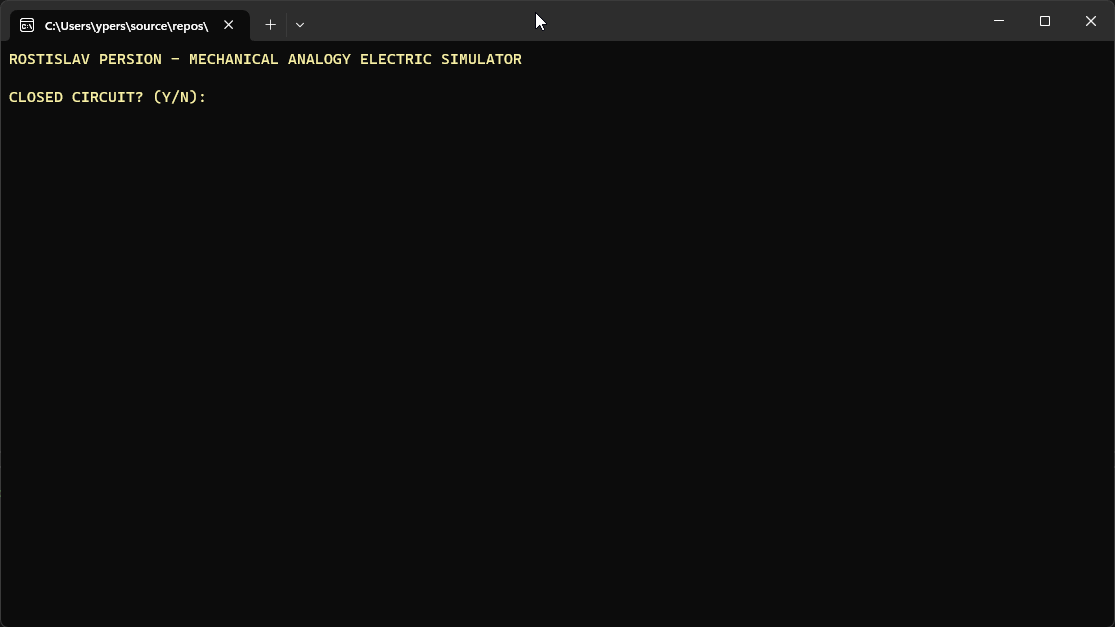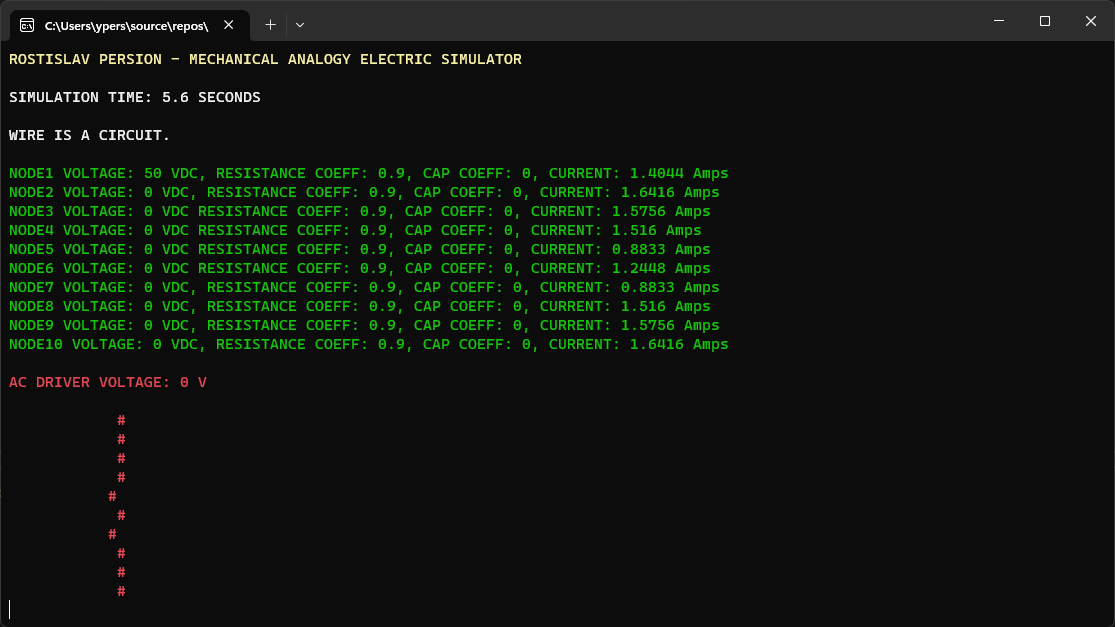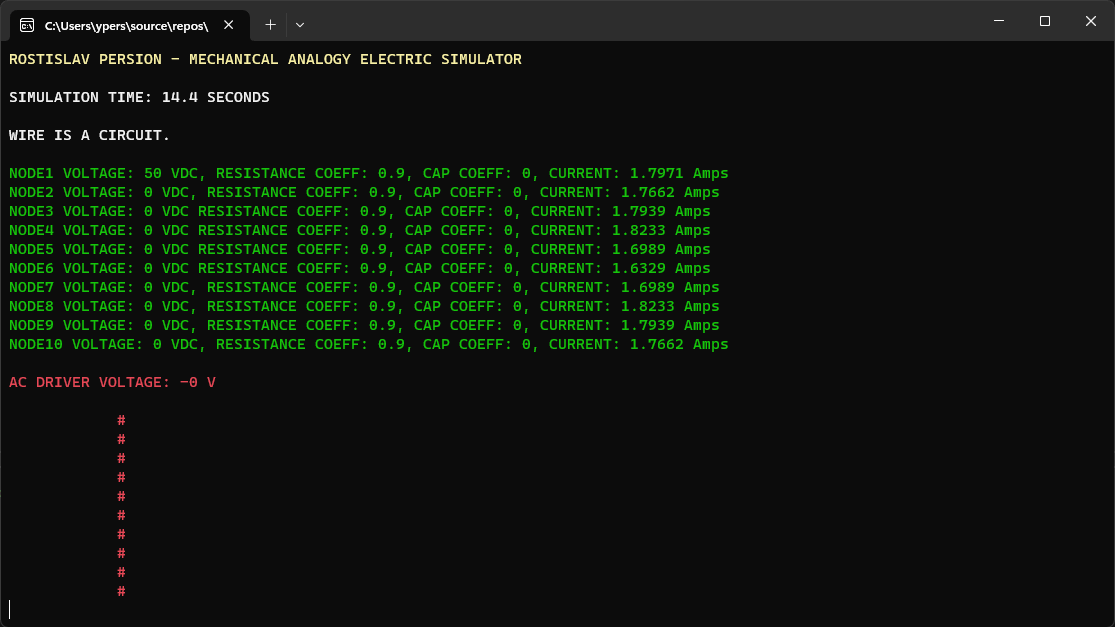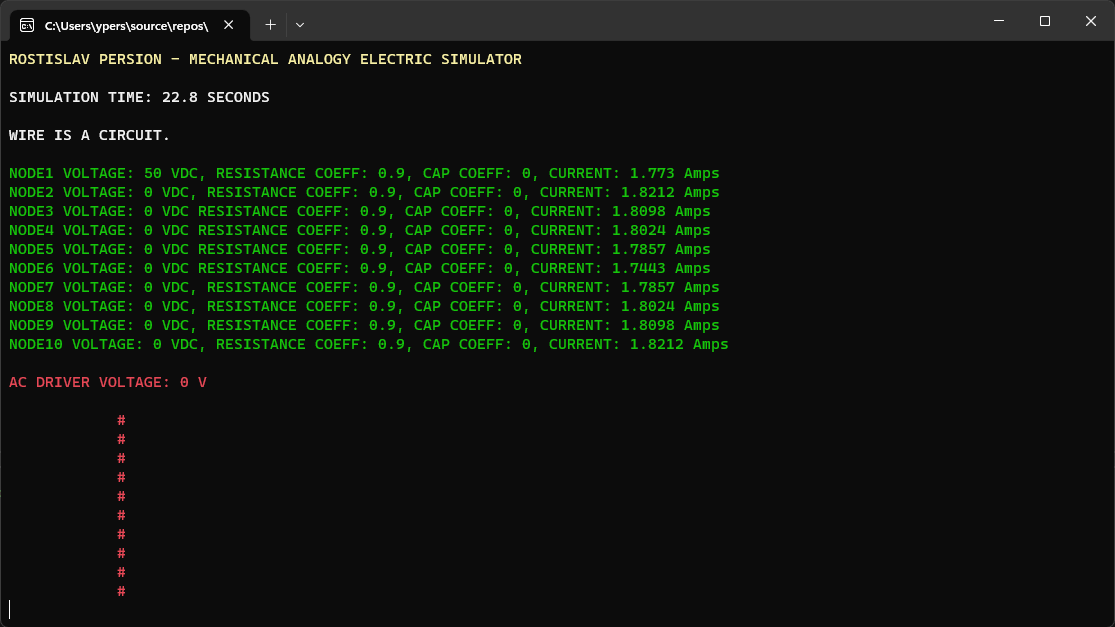
CLOSED CIRCUIT AC (# = NODE CURRENT) (TOP NODE IS AC DRIVER)
SOME SIMULATION VARIABLES WERE CHANGED IN THE CODE, NOT THE USER INPUT
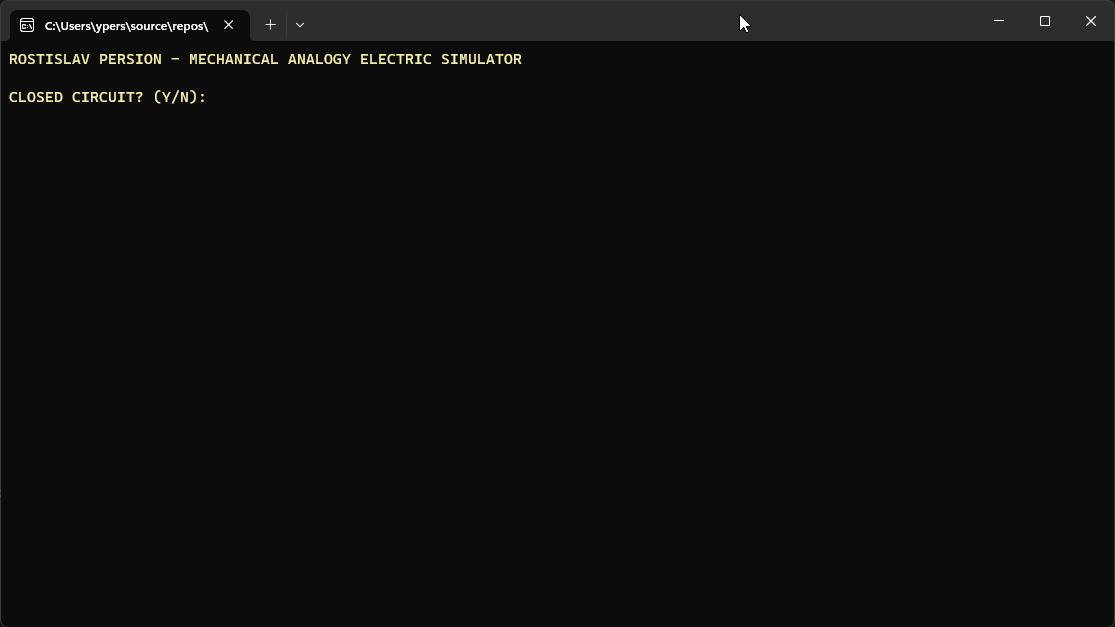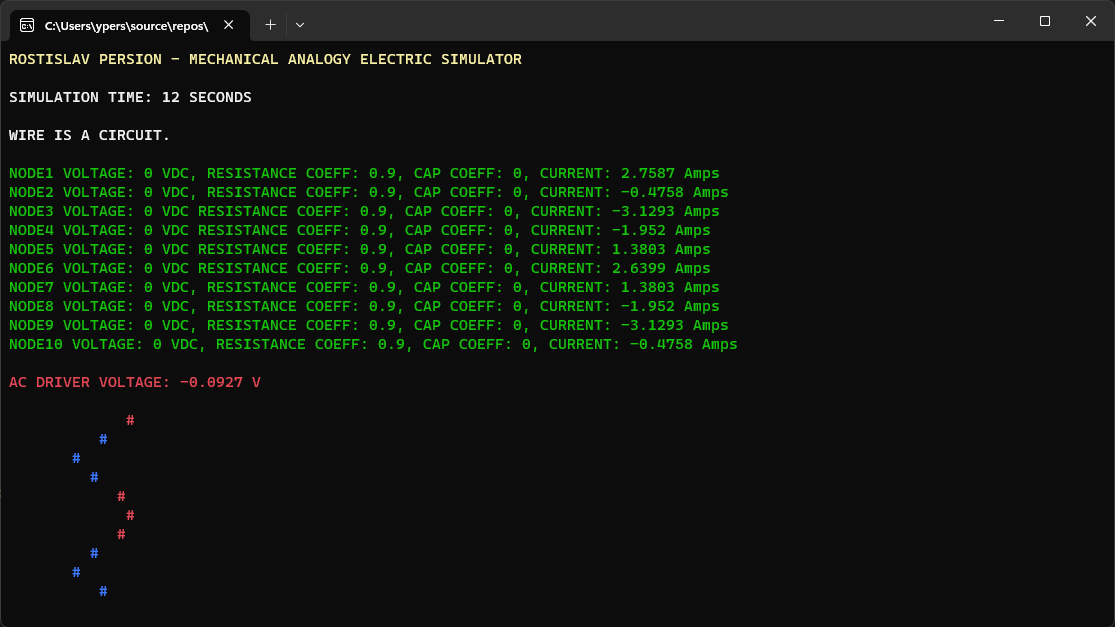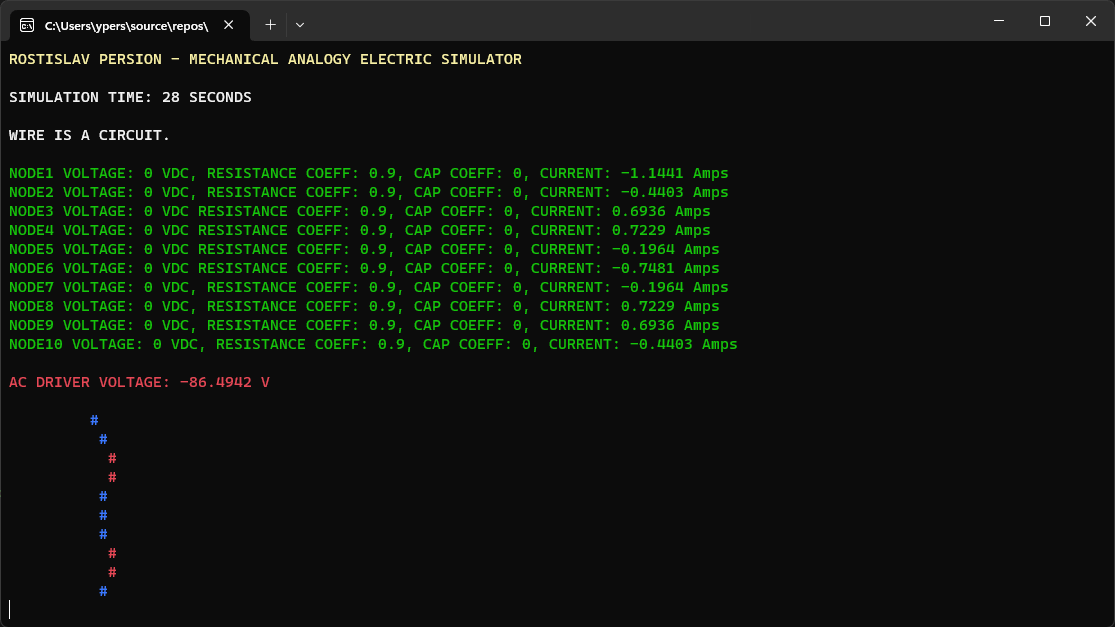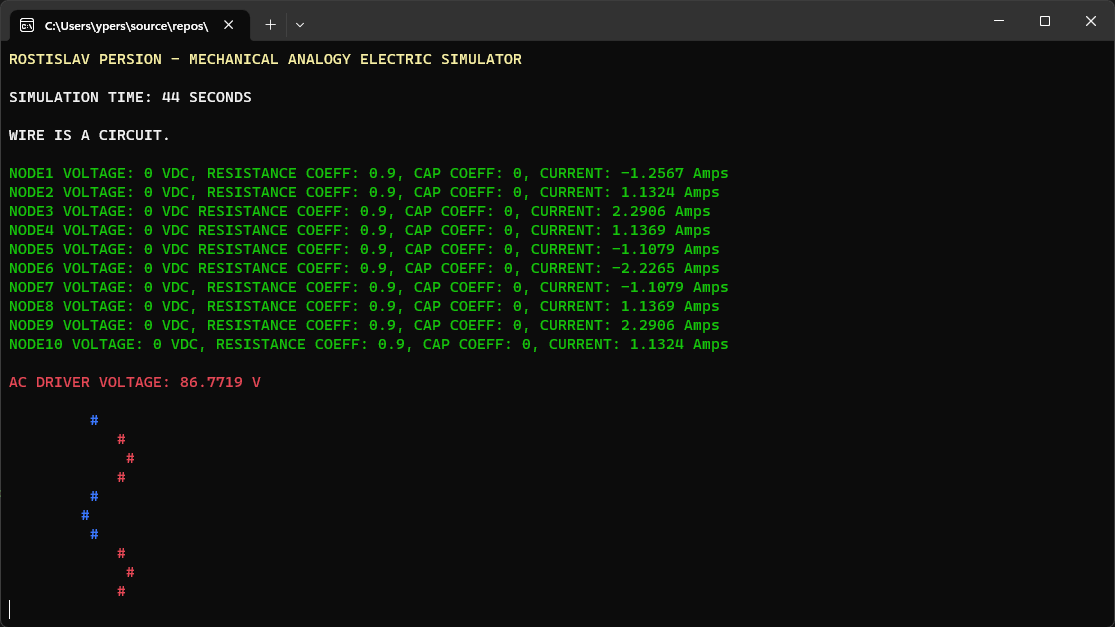
TRANSMISSION LINE WITH DUMMY LOAD (# = NODE CURRENT) (TOP NODE IS AC DRIVER, BOTTOM NODE IS DUMMY LOAD)
SOME SIMULATION VARIABLES WERE CHANGED IN THE CODE, NOT THE USER INPUT
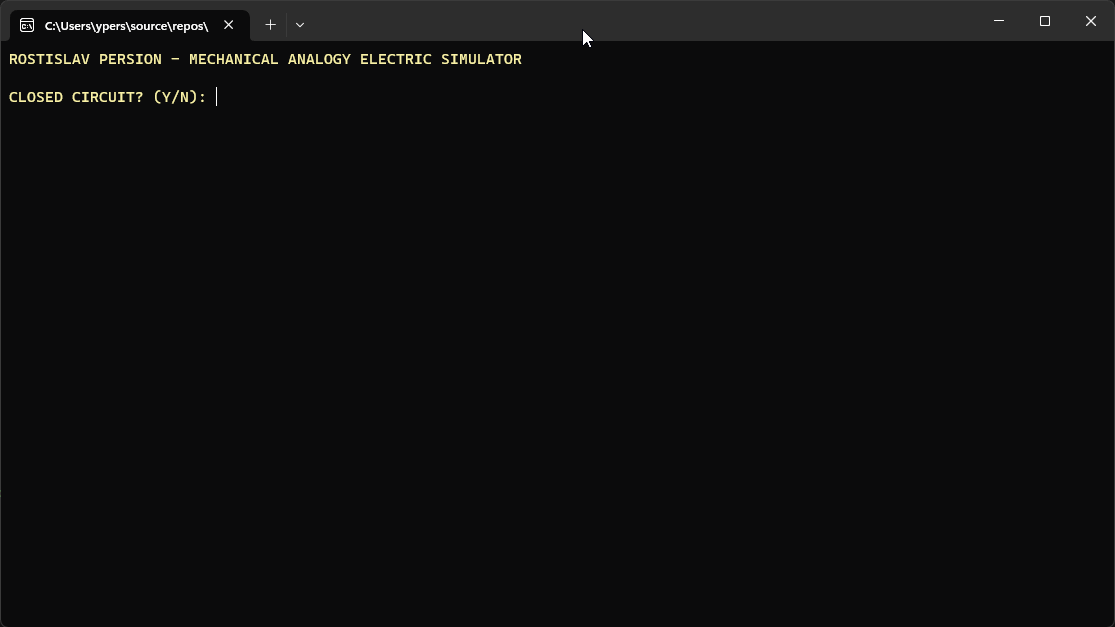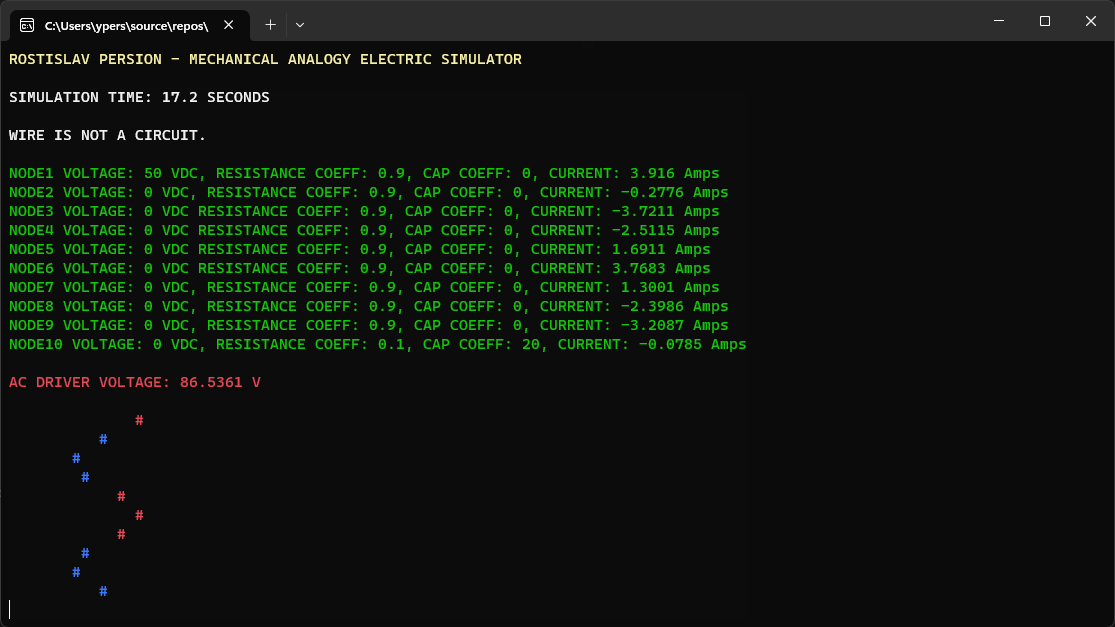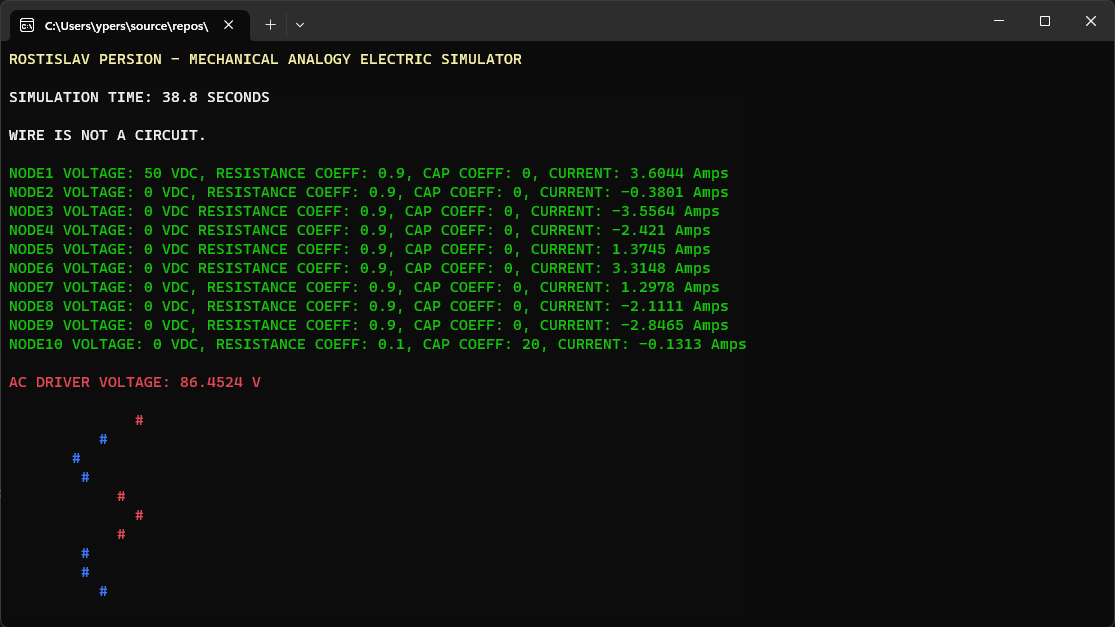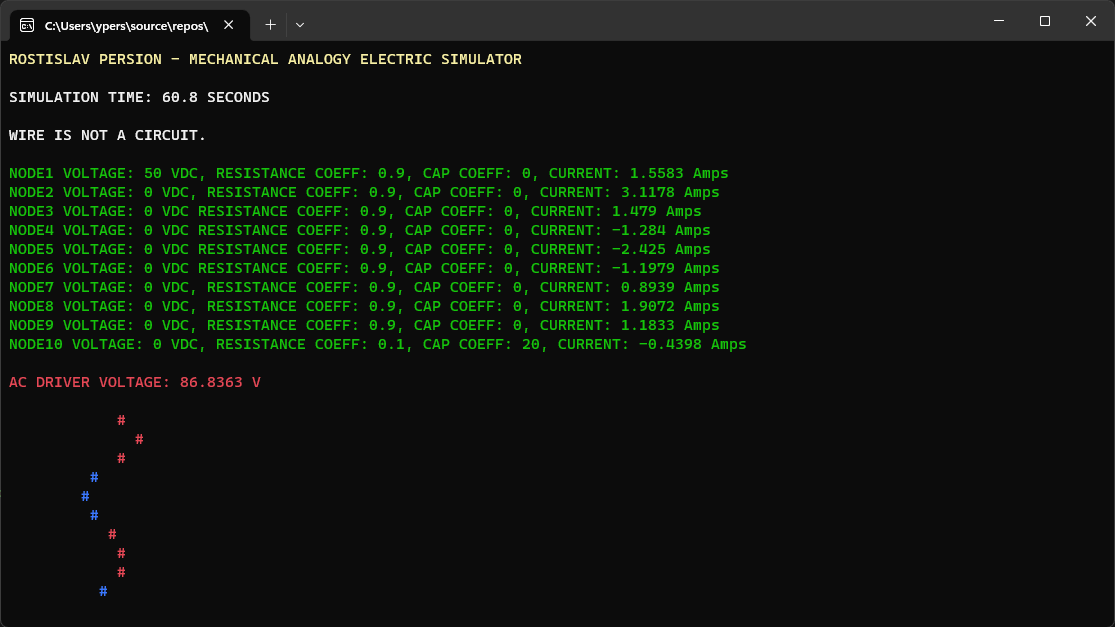
TRANSMISSION LINE WITH IMPEDANCE MISMATCH (# = NODE CURRENT) (TOP NODE IS AC DRIVER, BOTTOM NODE IS DUMMY LOAD)
TOP FIVE NODES HAVE DIFFERENT IMPEDANCE THAN BOTTOM FIVE NODES
SOME SIMULATION VARIABLES WERE CHANGED IN THE CODE, NOT THE USER INPUT
using System.Threading; namespace mec_elec_006 { class Mass { public double m = 5; public double x = 0; public double v; public double force = 0; public Spring spring; public double cap = 0; public double resistance = 0.99; public double voltage = 0; public void ConnectTo(Mass mass1, double k) { spring = new Spring(); spring.k = k; spring.mass = mass1; } } class Spring { public Mass mass; public double k = 1.2; } class Program { static void DrawGraph(double num) { double old_num = num; double base_line = 10; for (int i = 0; i < (num + base_line); i++) { Console.Write(" "); } if (old_num < 0) { Console.ForegroundColor = ConsoleColor.Blue; } else { Console.ForegroundColor = ConsoleColor.Red; } Console.Write("#"); Console.WriteLine(); } static void Main(string[] args) { // make circuit? Console.ForegroundColor = ConsoleColor.Yellow; Console.WriteLine("ROSTISLAV PERSION - MECHANICAL ANALOGY ELECTRIC SIMULATOR\n"); Console.Write("CLOSED CIRCUIT? (Y/N): "); string inp1 = Console.ReadLine(); bool circuit; if (inp1.Trim().ToUpper() == "Y") { circuit = true; } else { circuit = false; } //separator Console.WriteLine(); // AC input? Console.Write("AC INPUT? (volts) [100]: "); string inp2 = Console.ReadLine(); double AC_input = Convert.ToDouble(inp2); // create masses Mass m1 = new Mass(); Mass m2 = new Mass(); Mass m3 = new Mass(); Mass m4 = new Mass(); Mass m5 = new Mass(); Mass m6 = new Mass(); Mass m7 = new Mass(); Mass m8 = new Mass(); Mass m9 = new Mass(); Mass m10 = new Mass(); // create springs Spring sp1 = new Spring(); Spring sp2 = new Spring(); Spring sp3 = new Spring(); Spring sp4 = new Spring(); Spring sp5 = new Spring(); Spring sp6 = new Spring(); Spring sp7 = new Spring(); Spring sp8 = new Spring(); Spring sp9 = new Spring(); //loop back to one if (circuit) { Spring sp10 = new Spring(); } // connect masses and set spring const m1.ConnectTo(m2, 60); m2.ConnectTo(m3, 60); m3.ConnectTo(m4, 60); m4.ConnectTo(m5, 60); m5.ConnectTo(m6, 60); m6.ConnectTo(m7, 60); m7.ConnectTo(m8, 60); m8.ConnectTo(m9, 60); m9.ConnectTo(m10, 60); // connect back to one if (circuit) { m10.ConnectTo(m1, 60); } // set mass values m1.m = 10; m2.m = 10; m3.m = 10; m4.m = 10; m5.m = 10; m6.m = 10; m7.m = 10; m8.m = 10; m9.m = 10; m10.m = 10; // init capacitor, higher value = lower capacitor value m1.cap = 0; m2.cap = 0; m3.cap = 0; m4.cap = 0; m5.cap = 0; m6.cap = 0; m7.cap = 0; m8.cap = 0; m9.cap = 0; m10.cap = 0; // init voltage m1.voltage = 0; // init resistance (0 to 1) 0 = insulator, 1 = conductor m1.resistance = 0.9; m2.resistance = 0.9; m3.resistance = 0.9; m4.resistance = 0.9; m5.resistance = 0.9; m6.resistance = 0.9; m7.resistance = 0.9; m8.resistance = 0.9; m9.resistance = 0.9; m10.resistance = 0.9; double t = 0; double dt = 0.4; double ac_force = 0; while (true) { //update timer t += dt; // reset forces m1.force = 0; m2.force = 0; m3.force = 0; m4.force = 0; m5.force = 0; m6.force = 0; m7.force = 0; m8.force = 0; m9.force = 0; m10.force = 0; // AC input double freq = 150; ac_force = Math.Sin((t * freq) * (3.1415 / 180)) * AC_input; m1.force += ac_force; // calculate forces between masses, apply voltages m1.force += ((-(m1.x - m1.spring.mass.x) * m1.spring.k)) + m1.voltage; m2.force += ((m1.x - m1.spring.mass.x)) * m1.spring.k; m2.force += ((-(m2.x - m2.spring.mass.x) * m2.spring.k)) + m2.voltage; m3.force += ((m2.x - m2.spring.mass.x)) * m2.spring.k; m3.force += ((-(m3.x - m3.spring.mass.x) * m3.spring.k)) + m3.voltage; m4.force += ((m3.x - m3.spring.mass.x)) * m3.spring.k; m4.force += ((-(m4.x - m4.spring.mass.x) * m4.spring.k)) + m4.voltage; m5.force += ((m4.x - m4.spring.mass.x)) * m4.spring.k; m5.force += ((-(m5.x - m5.spring.mass.x) * m5.spring.k)) + m5.voltage; m6.force += ((m5.x - m5.spring.mass.x)) * m5.spring.k; m6.force += ((-(m6.x - m6.spring.mass.x) * m6.spring.k)) + m6.voltage; m7.force += ((m6.x - m6.spring.mass.x)) * m6.spring.k; m7.force += ((-(m7.x - m7.spring.mass.x) * m7.spring.k)) + m7.voltage; m8.force += ((m7.x - m7.spring.mass.x)) * m7.spring.k; m8.force += ((-(m8.x - m8.spring.mass.x) * m8.spring.k)) + m8.voltage; m9.force += ((m8.x - m8.spring.mass.x)) * m8.spring.k; m9.force += ((-(m9.x - m9.spring.mass.x) * m9.spring.k)) + m9.voltage; m10.force += ((m9.x - m9.spring.mass.x)) * m9.spring.k; //loop back to one if (circuit) { m10.force += ((-(m10.x - m10.spring.mass.x) * m10.spring.k)) + m10.voltage; m1.force += ((m10.x - m10.spring.mass.x)) * m10.spring.k; } // calculate capacitor if (m1.cap > 0) { m1.force += -m1.x * m1.cap; } if (m2.cap > 0) { m2.force += -m2.x * m2.cap; } if (m3.cap > 0) { m3.force += -m3.x * m3.cap; } if (m4.cap > 0) { m4.force += -m4.x * m4.cap; } if (m5.cap > 0) { m5.force += -m5.x * m5.cap; } if (m6.cap > 0) { m6.force += -m6.x * m6.cap; } if (m7.cap > 0) { m7.force += -m7.x * m7.cap; } if (m8.cap > 0) { m8.force += -m8.x * m8.cap; } if (m9.cap > 0) { m9.force += -m9.x * m9.cap; } if (m10.cap > 0) { m10.force += -m10.x * m10.cap; } // calculate velocities from force and mass m1.v += (m1.force / m1.m) * dt; m2.v += (m2.force / m2.m) * dt; m3.v += (m3.force / m3.m) * dt; m4.v += (m4.force / m4.m) * dt; m5.v += (m5.force / m5.m) * dt; m6.v += (m6.force / m6.m) * dt; m7.v += (m7.force / m7.m) * dt; m8.v += (m8.force / m8.m) * dt; m9.v += (m9.force / m9.m) * dt; m10.v += (m10.force / m10.m) * dt; // add frictiction m1.v = m1.v * m1.resistance; m2.v = m2.v * m2.resistance; m3.v = m3.v * m3.resistance; m4.v = m4.v * m4.resistance; m5.v = m5.v * m5.resistance; m6.v = m6.v * m6.resistance; m7.v = m7.v * m7.resistance; m8.v = m8.v * m8.resistance; m9.v = m9.v * m9.resistance; m10.v = m10.v * m10.resistance; // update mass location m1.x += m1.v * dt; m2.x += m2.v * dt; m3.x += m3.v * dt; m4.x += m4.v * dt; m5.x += m5.v * dt; m6.x += m6.v * dt; m7.x += m7.v * dt; m8.x += m8.v * dt; m9.x += m9.v * dt; m10.x += m10.v * dt; // console output Console.Clear(); Console.ForegroundColor = ConsoleColor.Yellow; // credits Console.WriteLine("ROSTISLAV PERSION - MECHANICAL ANALOGY ELECTRIC SIMULATOR\n"); Console.ForegroundColor = ConsoleColor.White; Console.WriteLine("SIMULATION TIME: " + Convert.ToString(Math.Round(t, 8)).Trim() + " SECONDS\n"); if (circuit) { Console.WriteLine("WIRE IS A CIRCUIT."); } else { Console.WriteLine("WIRE IS NOT A CIRCUIT."); } Console.ForegroundColor = ConsoleColor.Green; Console.WriteLine(); Console.Write("NODE1 VOLTAGE: " + Convert.ToString(Math.Round(m1.voltage, 4)).Trim() + " VDC"); Console.Write(", RESISTANCE COEFF: " + Convert.ToString(Math.Round(m1.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m1.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m1.v, 4)).Trim() + " Amps"); Console.Write("NODE2 VOLTAGE: " + Convert.ToString(Math.Round(m2.voltage, 4)).Trim() + " VDC"); Console.Write(", RESISTANCE COEFF: " + Convert.ToString(Math.Round(m2.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m2.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m2.v, 4)).Trim() + " Amps"); Console.Write("NODE3 VOLTAGE: " + Convert.ToString(Math.Round(m3.voltage, 4)).Trim() + " VDC"); Console.Write(" RESISTANCE COEFF: " + Convert.ToString(Math.Round(m3.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m3.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m3.v, 4)).Trim() + " Amps"); Console.Write("NODE4 VOLTAGE: " + Convert.ToString(Math.Round(m4.voltage, 4)).Trim() + " VDC"); Console.Write(" RESISTANCE COEFF: " + Convert.ToString(Math.Round(m4.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m4.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m4.v, 4)).Trim() + " Amps"); Console.Write("NODE5 VOLTAGE: " + Convert.ToString(Math.Round(m5.voltage, 4)).Trim() + " VDC"); Console.Write(" RESISTANCE COEFF: " + Convert.ToString(Math.Round(m5.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m5.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m5.v, 4)).Trim() + " Amps"); Console.Write("NODE6 VOLTAGE: " + Convert.ToString(Math.Round(m6.voltage, 4)).Trim() + " VDC"); Console.Write(" RESISTANCE COEFF: " + Convert.ToString(Math.Round(m6.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m6.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m6.v, 4)).Trim() + " Amps"); Console.Write("NODE7 VOLTAGE: " + Convert.ToString(Math.Round(m7.voltage, 4)).Trim() + " VDC"); Console.Write(", RESISTANCE COEFF: " + Convert.ToString(Math.Round(m7.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m7.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m7.v, 4)).Trim() + " Amps"); Console.Write("NODE8 VOLTAGE: " + Convert.ToString(Math.Round(m8.voltage, 4)).Trim() + " VDC"); Console.Write(", RESISTANCE COEFF: " + Convert.ToString(Math.Round(m8.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m8.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m8.v, 4)).Trim() + " Amps"); Console.Write("NODE9 VOLTAGE: " + Convert.ToString(Math.Round(m9.voltage, 4)).Trim() + " VDC"); Console.Write(", RESISTANCE COEFF: " + Convert.ToString(Math.Round(m9.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m9.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m9.v, 4)).Trim() + " Amps"); Console.Write("NODE10 VOLTAGE: " + Convert.ToString(Math.Round(m10.voltage, 4)).Trim() + " VDC"); Console.Write(", RESISTANCE COEFF: " + Convert.ToString(Math.Round(m10.resistance, 4)).Trim()); Console.Write(", CAP COEFF: " + Convert.ToString(Math.Round(m10.cap, 4)).Trim()); Console.WriteLine(", CURRENT: " + Convert.ToString(Math.Round(m10.v, 4)).Trim() + " Amps"); Console.WriteLine(); //show graph Console.ForegroundColor = ConsoleColor.Red; Console.WriteLine("AC DRIVER VOLTAGE: " + Math.Round(ac_force, 4).ToString() + " V\n"); DrawGraph(m1.v); DrawGraph(m2.v); DrawGraph(m3.v); DrawGraph(m4.v); DrawGraph(m5.v); DrawGraph(m6.v); DrawGraph(m7.v); DrawGraph(m8.v); DrawGraph(m9.v); DrawGraph(m10.v); Thread.Sleep(100); } } } }
MODEL 002 - RADIAL

